今日感冒在家剛好利用時間打一篇文章,天氣變冷了大家要多注意保暖阿。![]()
給定數字n,並列出n * n皇后所有可能。
4
[
[".Q..", // Solution 1
"...Q",
"Q...",
"..Q."],
["..Q.", // Solution 2
"Q...",
"...Q",
".Q.."]
]
這經典提我想很多人大概都知道解法,。
首先要先知道主要規則,每個皇后上下左右的行列和對角線都不能放置其它皇后,由此我們可以詳細列出規則來分析。
當在寫程式時走訪都是按照順序從第一個擺到最後一個,所以有些規則是不必要的,則可以排除。
以下方為例:
下面將皇后放置在第三層放置在第三個位置
第零層N..N..N.
第一層.N.N.N..
第二層..NNN...
第三層...Q....
第四層........
第五層........
第六層........
第七層........
下面將皇后放置在第三層放置在第四個位置
第零層.N..N..N
第一層..N.N.N.
第二層...NNN..
第三層....Q...
第四層........
第五層........
第六層........
第七層........
第三層放置在第三個位置(3, 3)
1.考慮第二點檢查第零層到第二層的第三個位置是否有皇后,(0, 3)、(1, 3)、(2, 3)。
2.考慮第三點檢查第零層到第二層的45度左上方是否有皇后,(0, 0)、(1, 1)、(2, 2)。
3.考慮第四點檢查第零層到第二層的45度右上方是否有皇后,(0, 6)、(1, 5)、(2, 4)。
第三層放置在第四個位置(3, 4)
1.考慮第二點檢查第零層到第二層的第四個位置是否有皇后,(0, 4)、(1, 4)、(2, 4)。
2.考慮第三點檢查第零層到第二層的45度左上方是否有皇后,(0, 1)、(1, 2)、(2, 3)。
3.考慮第四點檢查第零層到第二層的45度右上方是否有皇后,(0, 7)、(1, 6)、(2, 5)。
上述可得到:
但若仔細觀察第三和第四點的圖形或座標,可推倒出一個公式,若abs(放置位置 - N層放置位置) = (放置層 - N層)則代表已有皇后放置,接著直接來看一下如何推導出來。
第三層放置在第三個位置(3, 3)
第三層放置在第四個位置(3, 4)
由上可知道一公式,層數差K則abs(放置位置 - N層放置位置) = K。然而K為目前層數 - N層數。
CheckQueen:檢查上層是否有皇后。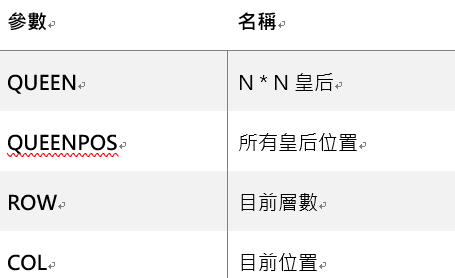
bool CheckQueen(const vector<string>& queen, const vector<int>& queenPos, const int row, const int col)
{
for (int index = 0; index < row; index++)
{
if (queenPos[index] == col
|| (row - index) == abs(col - queenPos[index]))
{
return false;
}
}
return true;
}
RunQueen:走訪每層並放置皇后。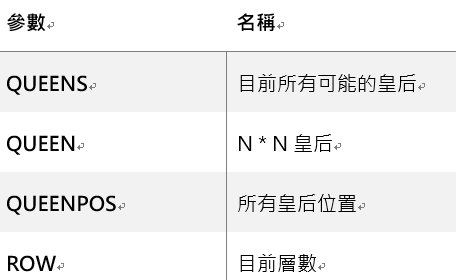
void RunQueen(vector<vector<string>>& queens, vector<string>& queen, vector<int>& queenPos, int row)
{
if (row == queen.size())
{
queens.push_back(queen);
return;
}
for (int index = 0; index < queen.size(); index++)
{
if (CheckQueen(queen, queenPos, row, index))
{
queen[row][index] = 'Q';
queenPos[row] = index;
RunQueen(queens, queen, queenPos, row + 1);
}
queen[row][index] = '.';
}
}
LeetCode呼叫方式。
vector<vector<string>> solveNQueens(int n) {
vector<vector<string>> queens;
vector<string> queen(n, string(n, '.'));
vector<int> queenPos(n);
RunQueen(queens, queen, queenPos, 0);
return queens;
}
經過解析希望每個人都能更加瞭解八皇后的公式由來,也祝大家假日愉快。
